
Fragment notatki:
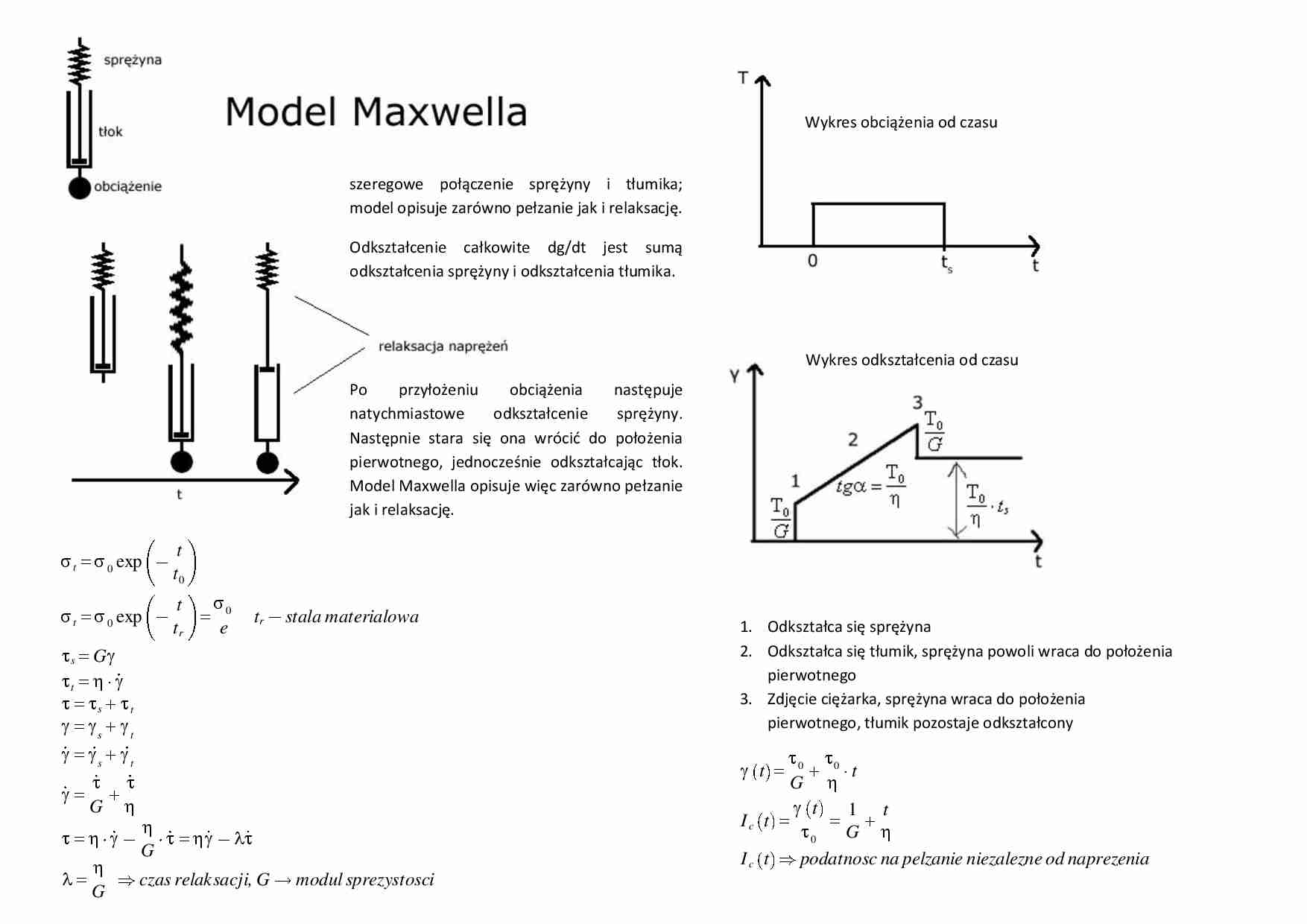
Wykres obciążenia od czasu
szeregowe połączenie sprężyny i tłumika;
model opisuje zarówno pełzanie jak i relaksację.
Odkształcenie całkowite dg/dt jest sumą
odkształcenia sprężyny i odkształcenia tłumika.
Wykres odkształcenia od czasu
Po
przyłożeniu
obciążenia
następuje
natychmiastowe
odkształcenie
sprężyny.
Następnie stara się ona wrócid do położenia
pierwotnego, jednocześnie odkształcając tłok.
Model Maxwella opisuje więc zarówno pełzanie
jak i relaksację.
t 0 exp
t
t0
t 0 exp
t
0
tr
e
tr
stala materialowa
s G
t
s t
s t
s t
G
G
1. Odkształca się sprężyna
2. Odkształca się tłumik, sprężyna powoli wraca do położenia
pierwotnego
3. Zdjęcie ciężarka, sprężyna wraca do położenia
pierwotnego, tłumik pozostaje odkształcony
0 0
t
G
t
1 t
Ic t
0
G
Ic t
podatnosc na pelzanie niezalezne od naprezenia
t
G
czas relaksacji, G
modul sprezystosci
Pelzanie
t 0 1 e
G
1
I t
1 e
G
s t
s t
G
t
0
G
0
Et
td
0
1
G
e
czas relaksacji
t
powrot poodksztalceniowy
t
t 0e
G
Wykres odkształcenia od czasu
slope
t
0
e
G
1
exp
t
td
odksztalcenie w chwili t
stala materialowa
t
t
Składa się on ze sprężyny, obrazującej sprężystośd, i tłumika hydraulicznego,
obrazującego lepkośd, połączonych ze sobą równolegle. W połączeniu równoległym
wydłużenie e sprężyny i tłumika są sobie równe, natomiast naprężenie s rozdziela
się na dwie części sS (w sprężynie) i st (w tłumiku). Przy natychmiastowym
przyłożeniu siły odkształcenie modelu będzie równe zeru, ponieważ tłumik nie daje
rozciągnięcia sprężyny i powstania odkształcenia. Z upływem czasu nastąpi jednak
przesunięcie tłocznika w tłumiku, związane z lepkością cieczy, a razem z nią może
rozciągad się sprężyna. W ten sposób stopniowo odkształcenie będzie narastad.
Model Kelvina - Voigta opisuje więc pełzanie (płynięcie mechaniczne) materiału
polimerowego. Nie opisuje relaksacji.
Deformacja nie rośnie w nieskooczonośd przy stałym T
Brak trwałego odkształcenia
Nie jest odpowiedni do opisu relaksacji
Ogólnie o modelach reologicznych
Są to układy tłumików i sprężyn połączonych ze sobą, przy
czym sprężyny opisują cechy sprężyste, a tłumiki cechy
lepkie. Sprężyna symbolizuje magazynowanie energii
odkształcenia, natomiast tłumiki rozpraszanie tej energii.
0
G1
0
t
s
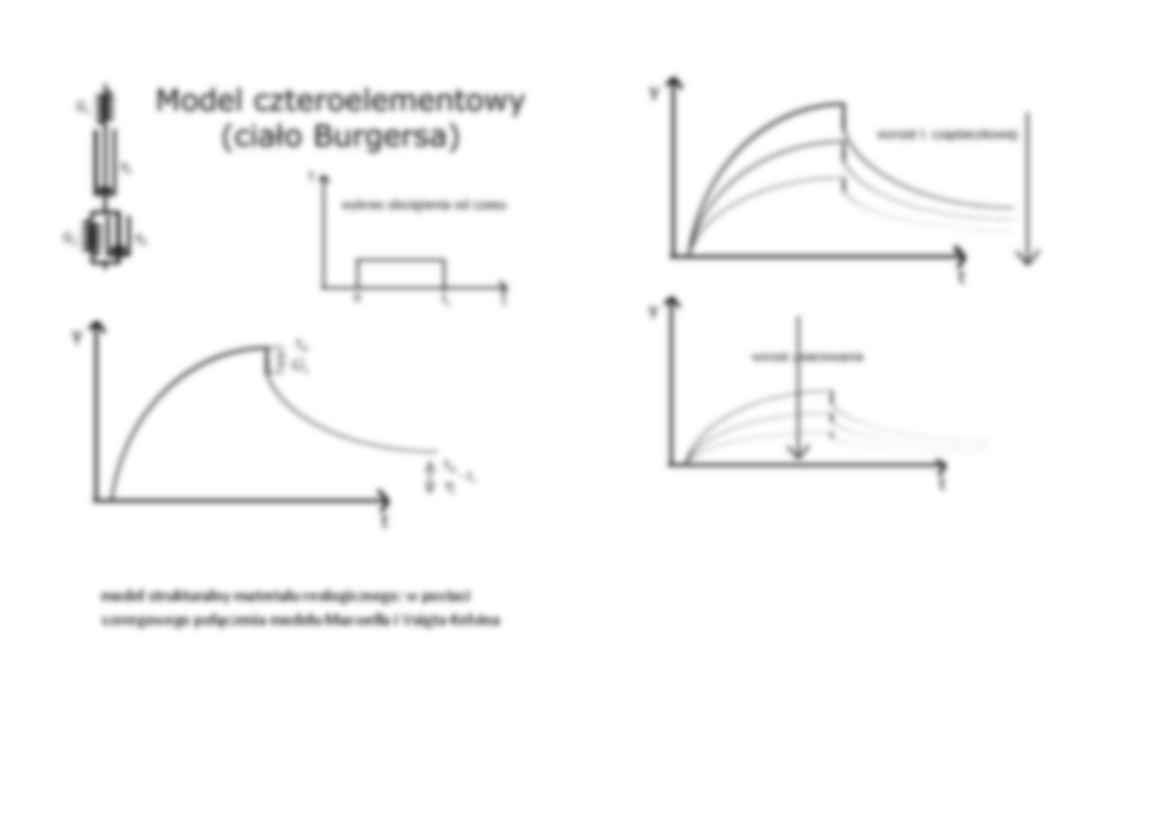
model strukturalny materiału reologicznego; w postaci
szeregowego połączenia modelu Maxwella i Voigta-Kelvina
Relaksacja naprężeo
Czas relaksacji λ
Zmiana naprężenia przy stałym odkształceniu
To czas po upływie którego naprężenie zmniejsza się e-krotnie (przy stałej
wartości odkształcenia)
0
0 e
t
t
Liniowa lepko sprężystość
G t
funkcja tylko t, nie zależy od tau i gamma
sprężyna
tłok
2τ0
τ0
2τ0/G(t)
τ0/G(t)
0 e
2τ0
τ0
0.37 0
Tgα=2τ0/η
Tgα=γ=τ0/η
t
Ge
t
Jak zachowa się materiał lepkosprężysty?
Cechy materiału
Skala czasu
De c
ts
G
Liczba Debory (Deborah number)
s stala materialu, ts skala czasu
Krótki czas relaksacji - szybki powrót poodkształceniowy
Długi czas relaksacji - zwolniony powrót
Kompozyty niekoniecznie muszą zawierać włókna!
(np. kompozyty proszkowe, pianki *kompozyty ciała stałego z gazem])
Deformacja i wzmocnienie w kompozytach z włóknem ciągłym
Rozważmy kompozyt obciążony siłą P równoległą do kierunku włókien
wzmacniających.
P C AC F AF M A M
Praktyczne wykorzystanie zjawiska – pomiary w strumieniu cieczy (?), balistyka,
elementy tłumiąc
Kompozyty
GFRP – Glass fibre reinforcement polymer
CFRP – carbon fibre reinforcement polymer
Matryca, osnowa - częśd układu, w której rozmieszczone są włókna.
Matryca zabezpiecza, zapewnia stałośd ułożenia włókien, matryca
transmituje (przenosi) naprężenia do wnętrza włókien, chroni włókna
przed szkodliwymi wpływami środowiska.
Włókna [elementy] wzmacniające – materiał pozwalający zoptymalizowad
właściwości kompozytu, zwłaszcza w odniesieniu do jednostek wagi
i kosztu.
XF
XM
fibre wlokno
naprezenie
matrix osnowa
A powierzchnia
XC
De1 relaksacja materiału jak u ciała sprężystego
De - 0 zachowanie zbliżone do cieczy
composite kompozyt
Przy równoległym ułożeniu włókien ich udział objętościowy wynosi
A
VF F
i stąd naprężenie przenoszone przez kompozyt
AC
C F V F M 1 V F
Wnioski:
Zbyt mała ilośd włókien może przynieśd więcej szkody niż pożytku
Aby uzyskad wzrost wytrzymałości zawartośd włókien powinna byd
większa od VF,kryt
Wytrzymałość kompozytu
Polimery
Podział ze względu na uporządkowanie łaocucha polimerowego
Amorficzne
Semikrystaliczne
Ciekłokrystaliczne
Polimery amorficzne
Struktura:
- makrocząsteczki bezładnie splątane w objętości materiału
- brak uporządkowania dalekiego zasięgu
- względnie brak relacji pomiędzy objętością swobodną materiału a jego
właściwościami (?)
W niskiej temperaturze i/lub szybkich odkształceniach twarde, kruche jak
szkło (ruchy molekularne całych łancuchów mają krótki zakres).
Po przekroczeniu temp. zeszklenia (lub w rezultacie zmniejszenie częstości
odkształceo) ruch molekularny całych łaocuchów (lub dużych fragmentów):
przejście od stanu szklistego w stan elastyczny (kauczukopodobny).
W jeszcze wyższej temp. zanika elastycznośd, pojawia się lepka ciecz.
Polimery semikrystaliczne
Zdolnośd do krystalizacji / budowy łaocucha
o Regularnośd, giętkośd, oddziaływania
międzyłaocuchowe
Stopieo krystalizacji %
o Wielocząsteczkowa budowa utrudnia krystalizację
o Dwufazowa budowa
ORIENTACJA POLIMERÓW
- dotyczy polimerów amorficznych i krystalicznych
- anizotropia właściwości wzdłuż i w poprzek kierunku orientacji
Typowe struktury polimerów o zorientowanych makrocząsteczkach:
a) Niezorientowany polimer amorficzny
b) Zorientowany polimer amorficzny
c) Polimer krystaliczny z przypadkowo rozmieszczonymi kryształami
d) Polimer krystaliczny ze zorientowanymi kryształami
... zobacz całą notatkę

Komentarze użytkowników (0)