To tylko jedna z 2 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
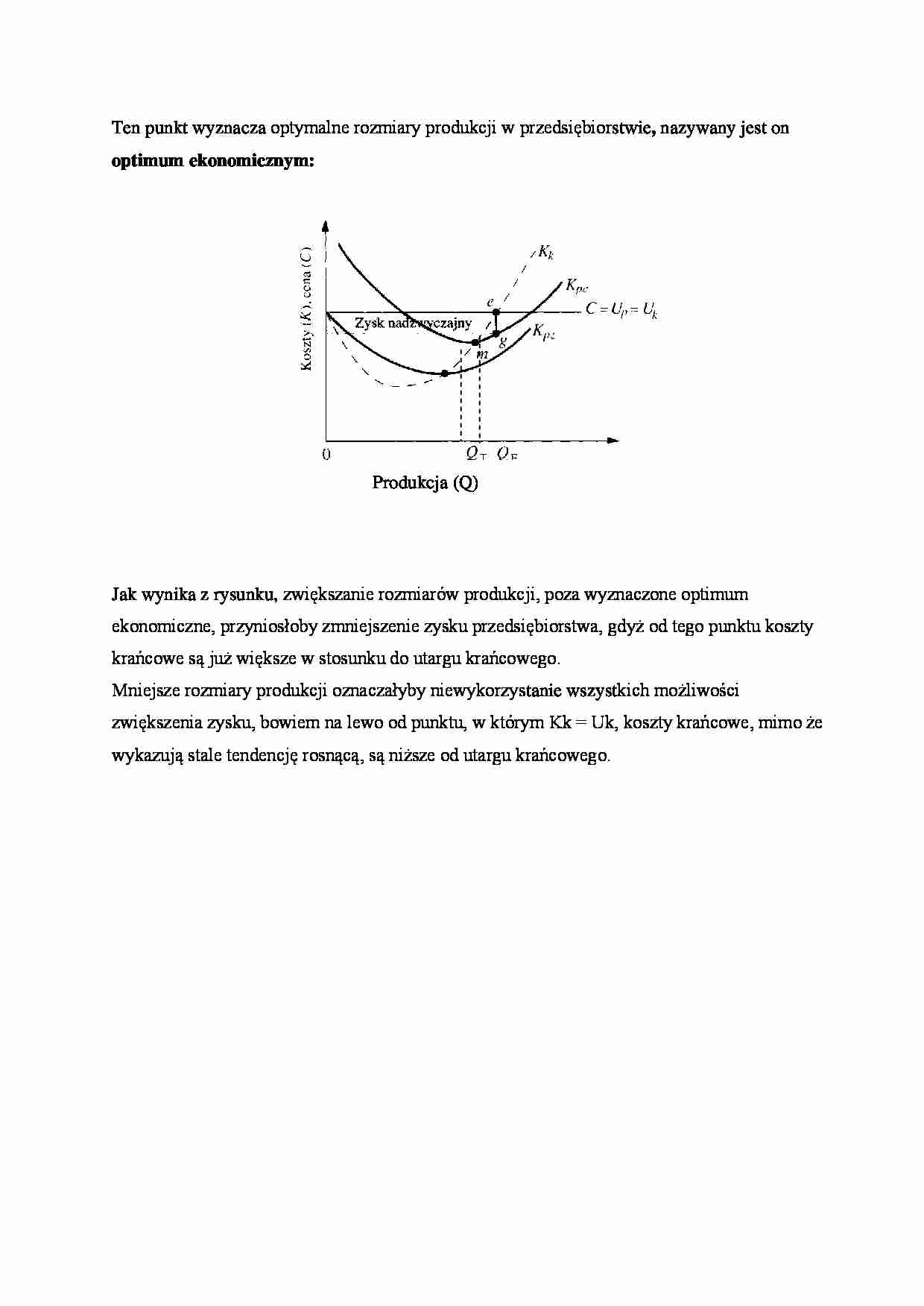

Ten punkt wyznacza optymalne rozmiary produkcji w przedsiębiorstwie, nazywany jest on optimum ekonomicznym:
Produkcja (Q)
Jak wynika z rysunku, zwiększanie rozmiarów produkcji, poza wyznaczone optimum ekonomiczne, przyniosłoby zmniejszenie zysku przedsiębiorstwa, gdyż od tego punktu koszty krańcowe są już większe w stosunku do utargu krańcowego.
Mniejsze rozmiary produkcji oznaczałyby niewykorzystanie wszystkich możliwości zwiększenia zysku, bowiem na lewo od punktu, w którym Kk = Uk, koszty krańcowe, mimo że wykazują stale tendencję rosnącą, są niższe od utargu krańcowego.
Zysk na jednostkę produkcji zj jest nadwyżką ceny C nad przeciętnymi kosztami całkowitymi Kpc.
Czyli: zj = C - Kpc Zysk całkowity Zc jest iloczynem zysku jednostkowego zj i ilości wytworzonej produkcji Q, czyli: Zc = zj · Q
lub: Zc = (C-Kpc) · Q
stąd: Zc = Uc - Kc
Zysk całkowity w przedsiębiorstwie jest dodatnią różnicą między utargiem całkowitym a kosztami całkowitymi. Jest on nazywany zyskiem nadzwyczajnym. Wynika on z korzystnego kształtowania się ceny (utargu przeciętnego) w stosunku do przeciętnych kosztów wytwarzania. Istnienie zysku nadzwyczajnego w warunkach doskonałej konkurencji oznacza, że przedsiębiorstwa znajdują się w korzystnej sytuacji ekonomicznej.
Zysk nadzwyczajny w przedsiębiorstwie występuje wówczas, gdy spełniony jest warunek: Kk = C Kpc Oznacza to, że cena musi się kształtować powyżej przeciętnego kosztu wytwarzania na jednostkę produkcji. Minimalny poziom kosztów jednostkowych wyraża równanie Kk = Kpc w punkcie m.
... zobacz całą notatkę




Komentarze użytkowników (0)