To tylko jedna z 5 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


Oligopol oferentów: ustalenie ceny przy heterogenicznej konkurencji. W konkurencji homogenicznej zakładaliśmy, że produkty wytwarzane przez kilku producentów są nierozróżnialne dla nabywców, czyli nie mają oni żadnych preferencji w stosunku do oferentów. Teraz będziemy rozpatrywać przypadek, gdy nabywcy rozróżniają wyroby poszczególnych producentów i są gotowi płacić różne ceny za te wyroby, które są w stosunku do siebie blisko substytucyjne.
1. Załamana krzywa cena-zbyt
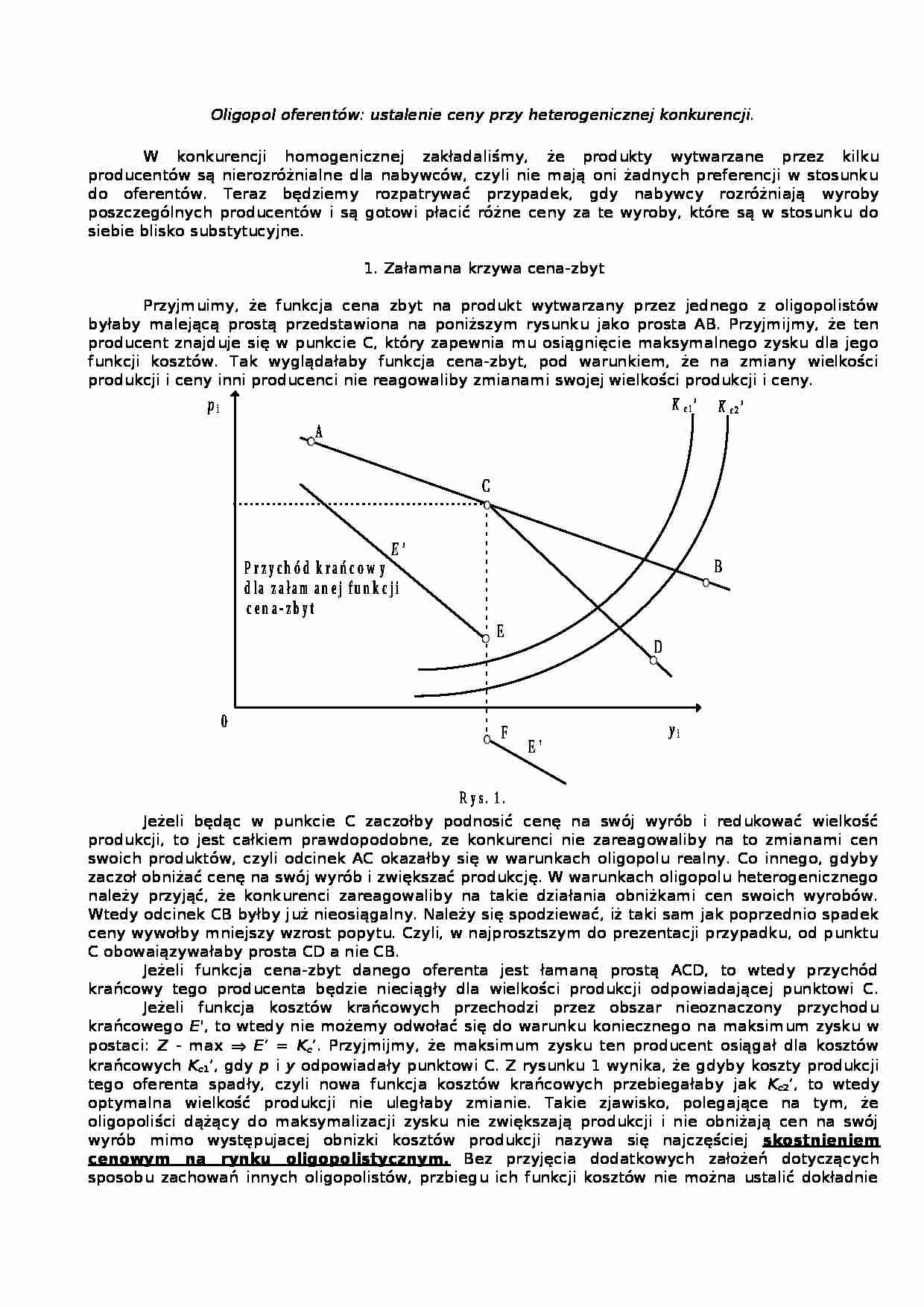
Przyjmuimy, że funkcja cena zbyt na produkt wytwarzany przez jednego z oligopolistów byłaby malejącą prostą przedstawiona na poniższym rysunku jako prosta AB. Przyjmijmy, że ten producent znajduje się w punkcie C, który zapewnia mu osiągnięcie maksymalnego zysku dla jego funkcji kosztów. Tak wyglądałaby funkcja cena-zbyt, pod warunkiem, że na zmiany wielkości produkcji i ceny inni producenci nie reagowaliby zmianami swojej wielkości produkcji i ceny.
Jeżeli będąc w punkcie C zaczołby podnosić cenę na swój wyrób i redukować wielkość produkcji, to jest całkiem prawdopodobne, ze konkurenci nie zareagowaliby na to zmianami cen swoich produktów, czyli odcinek AC okazałby się w warunkach oligopolu realny. Co innego, gdyby zaczoł obniżać cenę na swój wyrób i zwiększać produkcję. W warunkach oligopolu heterogenicznego należy przyjąć, że konkurenci zareagowaliby na takie działania obniżkami cen swoich wyrobów. Wtedy odcinek CB byłby już nieosiągalny. Należy się spodziewać, iż taki sam jak poprzednio spadek ceny wywołby mniejszy wzrost popytu. Czyli, w najprosztszym do prezentacji przypadku, od punktu C obowaiązywałaby prosta CD a nie CB.
Jeżeli funkcja cena-zbyt danego oferenta jest łamaną prostą ACD, to wtedy przychód krańcowy tego producenta będzie nieciągły dla wielkości produkcji odpowiadającej punktowi C. Jeżeli funkcja kosztów krańcowych przechodzi przez obszar nieoznaczony przychodu krańcowego E' , to wtedy nie możemy odwołać się do warunku koniecznego na maksimum zysku w postaci: Z - max E ' = K c '. Przyjmijmy, że maksimum zysku ten producent osiągał dla kosztów krańcowych K c 1 ', gdy p i y odpowiadały punktowi C. Z rysunku 1 wynika, że gdyby koszty produkcji tego oferenta spadły, czyli nowa funkcja kosztów krańcowych przebiegałaby jak K c 2 ', to wtedy optymalna wielkość produkcji nie uległaby zmianie. Takie zjawisko, polegające na tym, że oligopoliści dążący do maksymalizacji zysku nie zwiększają produkcji i nie obniżają cen na swój wyrób mimo występujacej obnizki kosztów produkcji nazywa się najczęściej skostnieniem cenowym na rynku oligopolistycznym. Bez przyjęcia dodatkowych założeń dotyczących sposobu zachowań innych oligopolistów, przbiegu ich funkcji kosztów nie można ustalić dokładnie jaki stan równowagi ukształtuje się na tym rynku. Opisany wyżej przypadek należy potraktować jako przyczynek. Pełniejsza analiza będzie przedstawiona w następnym punkcie.
(…)
… będzie przedstawiona w następnym punkcie.
2. Heterogeniczny duopol cenowy.
Poszerzone rozwiązanie Cournota i von Stackelberga.
Z poprzednich modeli Cournota i Stackelberga obowiązują nadal założenie, że
Dla uproszczenia analizy przyjmijmy następujące założenia:
1. Na rynku istniej tylko dwóch producentów, którzy zachowują się autonomicznie.
2. Nabywcy rozróżniają produkty wytwarzane przez tych dwóch producentów…
… musi być bardziej stroma niż proste cena-zbyt określone dla ceny p2 równej 0, 10 bądź 20.
Jeżeli teraz wykreślimy izolinie zysku identycznie jak to czyniliśmy w modelu Cournota, czy Stackelberga to możemy na każdej prostej cena-zbyt znaleźć taki punkt, który maksymalizuje zysk 1 producenta. Prezentuja to np. punkty R i S. Jeżeli chcemy znaleźć punkt maksymalizujący zysk na ostatniej (najbardziej oddalonej od poczatku…
… przeprowadzimy dla drugiego duopolisty i zechcemy umieścić je w takim jak ostatnio układzie współrzędnych, to na rysunku można to przedstawić następująco, co prezentuje rys. 4.
Jeżeli tak jak na poczatku założyliśmy obaj producenci będą zachowywać się autonomicznie, to wtedy obaj po pewnym czasie dojdą do punktu V i ustalą ceny mu odpowiadające. Tym samym zrealizują zyski przypisdane izoliniom zysku…
... zobacz całą notatkę






Komentarze użytkowników (0)