To tylko jedna z 3 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
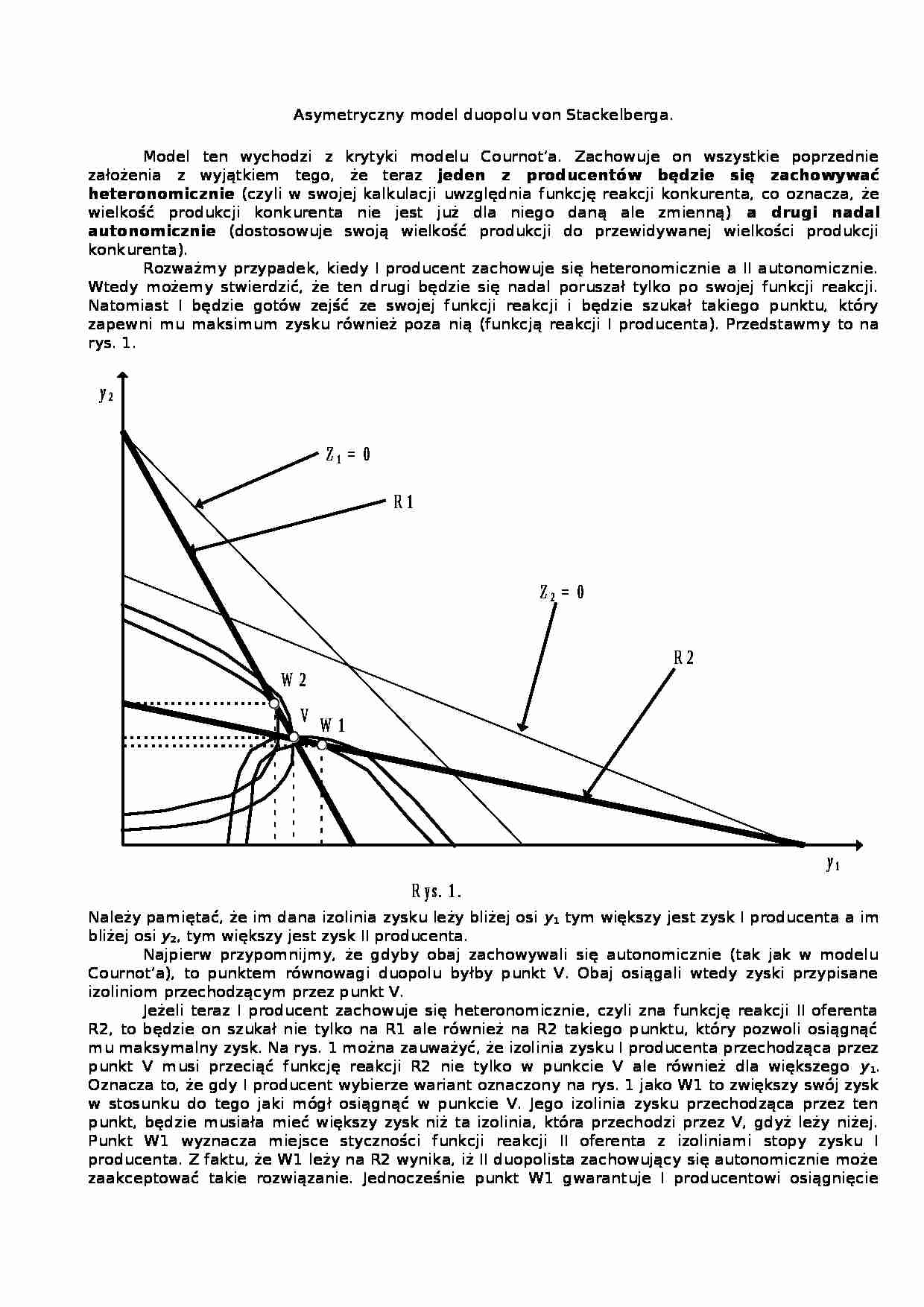


Asymetryczny model duopolu von Stackelberga. Model ten wychodzi z krytyki modelu Cournot'a. Zachowuje on wszystkie poprzednie założenia z wyjątkiem tego, że teraz jeden z producentów będzie się zachowywać heteronomicznie (czyli w swojej kalkulacji uwzględnia funkcję reakcji konkurenta, co oznacza, że wielkość produkcji konkurenta nie jest już dla niego daną ale zmienną) a drugi nadal autonomicznie (dostosowuje swoją wielkość produkcji do przewidywanej wielkości produkcji konkurenta).
Rozważmy przypadek, kiedy I producent zachowuje się heteronomicznie a II autonomicznie. Wtedy możemy stwierdzić, że ten drugi będzie się nadal poruszał tylko po swojej funkcji reakcji. Natomiast I będzie gotów zejść ze swojej funkcji reakcji i będzie szukał takiego punktu, który zapewni mu maksimum zysku również poza nią (funkcją reakcji I producenta). Przedstawmy to na rys. 1.
Należy pamiętać, że im dana izolinia zysku leży bliżej osi y 1 tym większy jest zysk I producenta a im bliżej osi y 2 , tym większy jest zysk II producenta. Najpierw przypomnijmy, że gdyby obaj zachowywali się autonomicznie (tak jak w modelu Cournot'a), to punktem równowagi duopolu byłby punkt V. Obaj osiągali wtedy zyski przypisane izoliniom przechodzącym przez punkt V.
Jeżeli teraz I producent zachowuje się heteronomicznie, czyli zna funkcję reakcji II oferenta R2, to będzie on szukał nie tylko na R1 ale również na R2 takiego punktu, który pozwoli osiągnąć mu maksymalny zysk. Na rys. 1 można zauważyć, że izolinia zysku I producenta przechodząca przez punkt V musi przeciąć funkcję reakcji R2 nie tylko w punkcie V ale również dla większego y 1 . Oznacza to, że gdy I producent wybierze wariant oznaczony na rys. 1 jako W1 to zwiększy swój zysk w stosunku do tego jaki mógł osiągnąć w punkcie V. Jego izolinia zysku przechodząca przez ten punkt, będzie musiała mieć większy zysk niż ta izolinia, która przechodzi przez V, gdyż leży niżej. Punkt W1 wyznacza miejsce styczności funkcji reakcji II oferenta z izoliniami stopy zysku I producenta. Z faktu, że W1 leży na R2 wynika, iż II duopolista zachowujący się autonomicznie może zaakceptować takie rozwiązanie. Jednocześnie punkt W1 gwarantuje I producentowi osiągnięcie największego zysku spośród wszystkich rozwiązań zawartych w ramach R1 i R2. Punkt W1 w stosunku do V różni się wielkościami produkcji y 1 i y 2 . Produkcja I oferenta wzrośnie a II zmaleje. Na podstawie rys. 1 możemy również stwierdzić, że zysk II producenta zmniejszy się w porównaniu do tego jaki osiągał w punkcie V.
Może postać pytanie dlaczego II producent zgodzi się na taką zmianę? Aby to wyjaśnić trzeba przypomnieć, że II producent zachowuje się autonomicznie, czyli tak dostosowuje swoją wielkość produkcji do produkcji konkurenta aby w tych warunkach osiągnąć maksymalny zysk. Jeżeli więc I oferent ustali swoją wielkość produkcji na poziomie
(…)
… w literaturze mianem dylematu więźnia. Bez wchodzenia w szczegóły rozwiązania tego typu gry należy stwierdzić, że ostateczny podział rynku będzie odzwierciedlał siłę przetargową obu producentów. Słabszy przedsiębiorca najprawdopodobniej będzie się zachowywał autonomicznie, bojąc się bardzej strat, jake poniósłby zachowując się heteronomicznie przy takim samym zachowaniu się konkurenta. Umożliwi tym samym…
… zysku zostanie osiągnięte, gdy produkcja tak zostanie podzielona między oba przedsiębiorstwa, że koszty krańcowe w obu firmach będą sobie równe i dodatkowo muszą odpowiadać przychodowi krańcowemu.
…
... zobacz całą notatkę






Komentarze użytkowników (0)