Całka podwójna w obszarze normalnym

W materiale znajdują się również przykłady liczbowe odnośnie całek.
                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                  

(…)

… CAŁKA PODWÓJNA W OBSZARZE NORMALNYM
Definicja (obszaru normalnego)
__
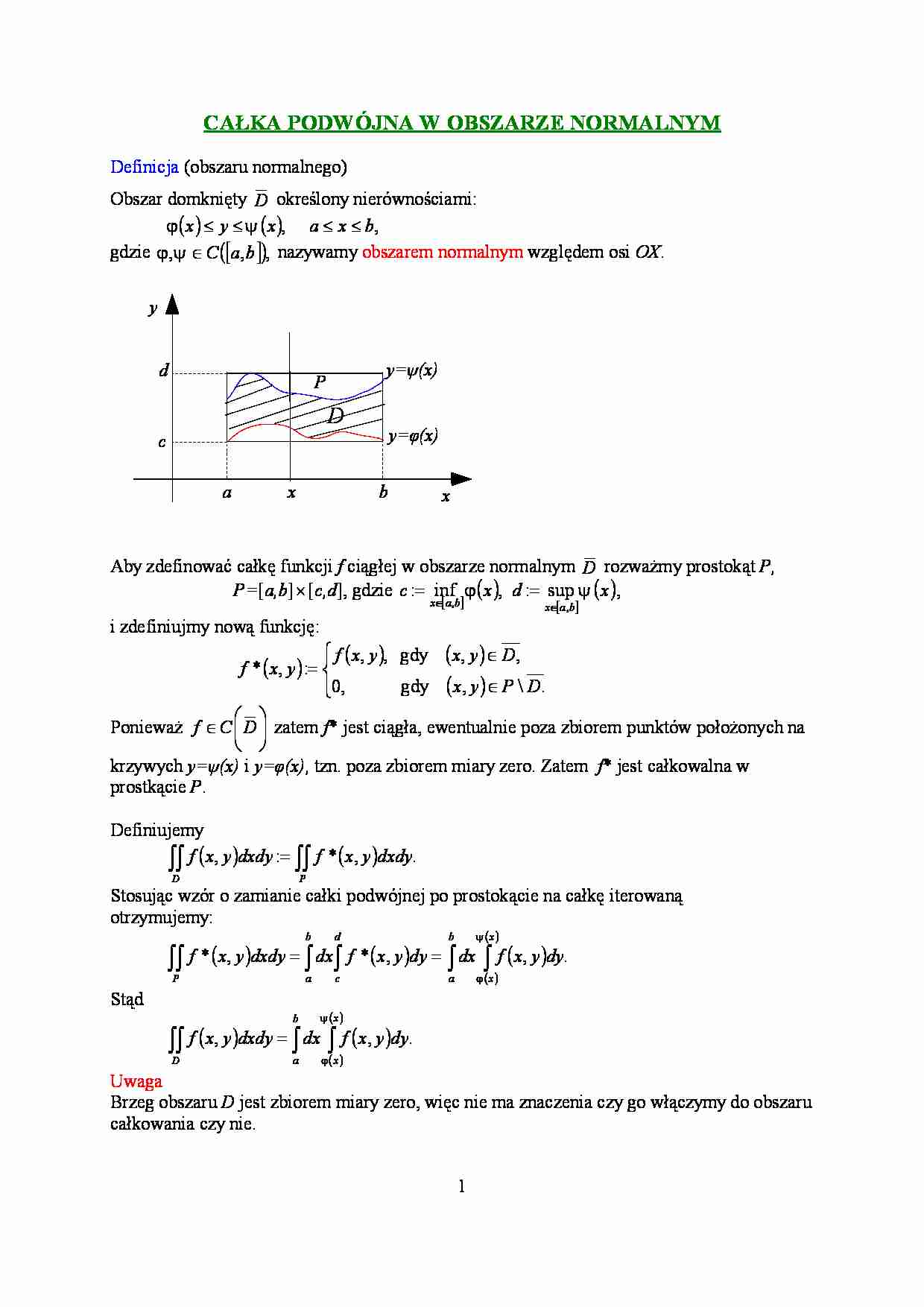
Obszar domknięty D określony nierównościami:
  x   y    x , a  x  b,
gdzie  ,  C a, b, nazywamy obszarem normalnym względem osi OX.
y
d
y=ψ(x)
P
D
c
a
x
y=φ(x)
b
x
__
Aby zdefinować całkę funkcji f ciągłej w obszarze normalnym D rozważmy prostokąt P,
P=[a,b] [c,d], gdzie c : inf   x , d : sup   x ,
x…
…    y , c  y  d ,
gdzie  ,   C c, d , nazywamy obszarem normalnym względem osi OY.
y
d
x=α(y)
x=β(y)
D
c
x
Analogicznie określamy całkę funkcji ciągłej w obszarze D normalnym względem OY i
wtedy

D
d
 y
c
 y
f  x, y dxdy   dy
 f x, y dx.
Definicja
Obszar dokmnięty D nazywamy obszarem regularnym, jeśli jest sumą
D  D 1  D 2  ...  D n obszarów normalnych względem osi OX…
… , gdzie D – obszar ograniczony krzywymi x  2 y 2
D
i x  y 2  1.
Wyznaczamy punkty (x,y) przecięcia parabol x  2 y 2 i x  y 2  1 :
y  1,
x  2.
i zaznaczamy obszar D
D jest obszarem normalnym względem OY,
 1  y  1
D: 2
2
2 y  x  y  1
Zatem możemy całkę podwójną zamienić na całkę iterowaną:
1
I   dy
1
y 2 1
1
 dx   x
1
2 y2
y 2 1
1
1
dy 
1

 1  y dy   y  3 y
2

1
2 y2
3
2…
... zobacz całą notatkę