To tylko jedna z 7 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
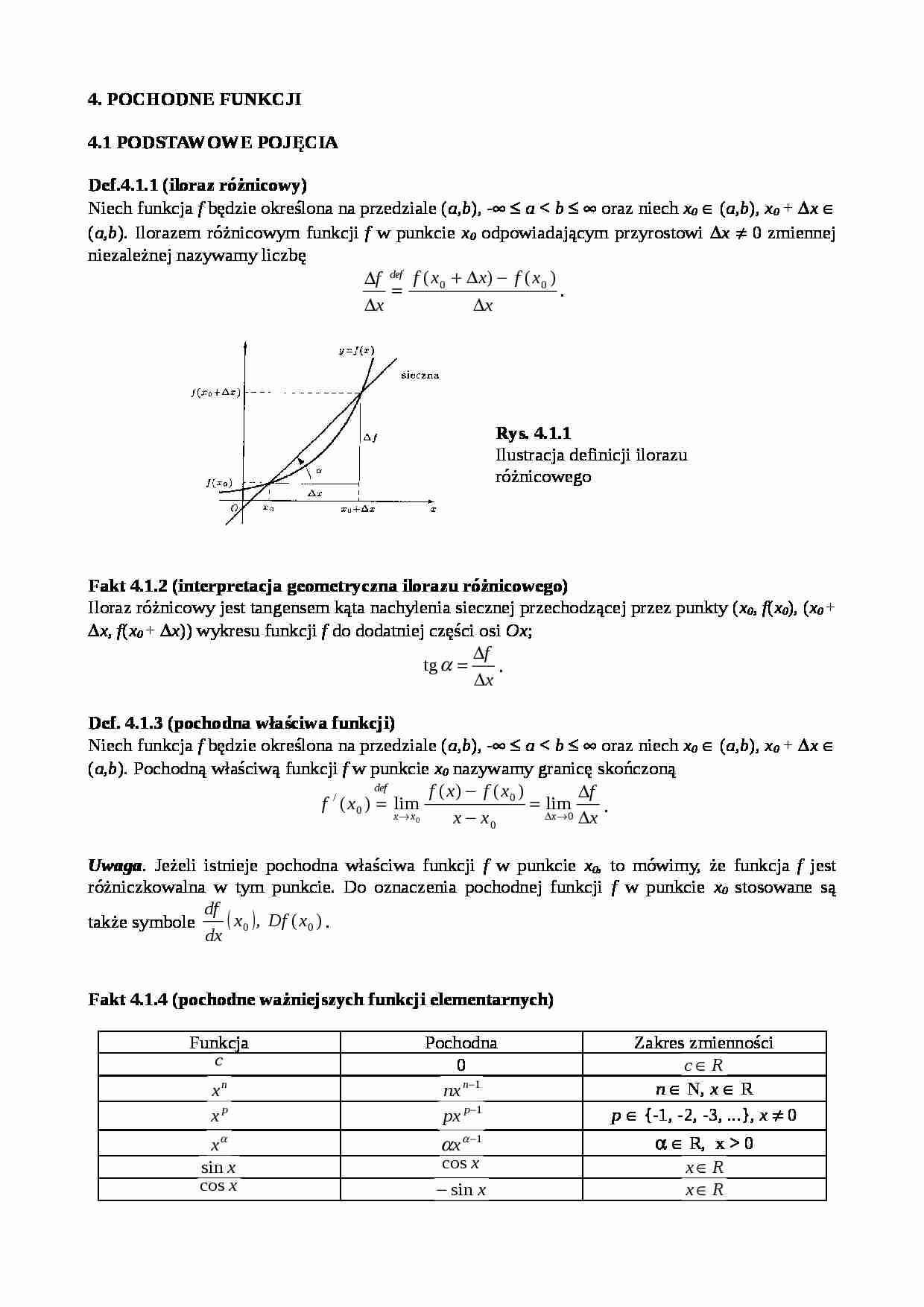


4. POCHODNE FUNKCJI 4.1 PODSTAWOWE POJĘCIA Def.4.1.1 (iloraz różnicowy) Niech funkcja f będzie określona na przedziale ( a , b ), - a 0
Funkcja
Pochodna
Zakres zmienności
0 0
Uwaga . Do obliczania pochodnych funkcji postaci oraz stosujemy wzory:
Def. 4.1.5 (styczna do wykresu funkcji) Niech funkcja f będzie określona na przedziale ( a , b ), - a
(…)
… funkcji wektorowej)
Niech , gdzie t (,), będzie funkcją wektorową. Pochodną funkcji w punkcie t określamy wzorem:
.
Podobnie określamy pochodną funkcji wektorowej , a także pochodne wyższych rzędów takich funkcji.
Fakt 4.5.5 (interpretacja fizyczna pochodnej funkcji wektorowej)
Niech oznacza wektor wodzący punktu materialnego w chwili t [t0,t1]. Wektor prędkości tego punktu wyraża się wzorem…
…. Jeżeli istnieje pochodna właściwa funkcji f w punkcie x0, to mówimy, że funkcja f jest różniczkowalna w tym punkcie. Do oznaczenia pochodnej funkcji f w punkcie x0 stosowane są także symbole .
Fakt 4.1.4 (pochodne ważniejszych funkcji elementarnych)
Funkcja
Pochodna
Zakres zmienności
0
n N, x R
p {-1, -2, -3, ...}, x 0
R, x > 0
Funkcja
Pochodna
Zakres zmienności
0 < a 1, x R
x 0
0 < a 1, x…
… jest także analogiczny wzór dla dowolnej liczby składanych funkcji oraz dla pochodnych jednostronnych funkcji złożonej.
Tw. 4.3.3 (o pochodnej funkcji odwrotnej)
Niech
funkcja f będzie ciągła na przedziale (a,b),
funkcja f będzie malejąca albo rosnąca na przedziale (a,b),
.
Wtedy funkcja odwrotna jest różniczkowalna w punkcie y0 = f(x0) oraz
.
Uwaga. Wzór ten jest prawdziwy także dla pochodnych jednostronnych właściwych i niewłaściwych.
Fakt 4.3.4 (pochodna funkcji elementarnej)
Pochodne funkcji elementarnych są funkcjami elementarnymi.
4.4 RÓŻNICZKA FUNKCJI
Def. 4.4.1 (różniczka funkcji)
Niech funkcja f ma pochodną właściwą w punkcie x0. Różniczką funkcji f w punkcie x0 nazywamy funkcję df zmiennej określoną wzorem
.
Fakt 4.4.2 (zastosowanie różniczki do obliczania przyrostu funkcji)
Niech funkcja f będzie różniczkowalna w punkcie x0. Wtedy
.
Fakt 4.4.3 (zastosowanie różniczki do szacowania błędów pomiarów)
Niech wielkości fizyczne x i y będą związane zależnością y = f(x). Ponadto niech x oznacza błąd bezwzględny pomiaru wielkości x. Wtedy błąd bezwzględny y obliczanej wielkości y wyraża się wzorem przybliżonym
,
gdzie x0 jest wynikiem pomiaru wielkości x.
Tw. 4.4.4 (o wielkości błędu w rachunkach przybliżonych…
… funkcji wektorowej)
Niech , gdzie t (,), będzie funkcją wektorową. Pochodną funkcji w punkcie t określamy wzorem:
.
Podobnie określamy pochodną funkcji wektorowej , a także pochodne wyższych rzędów takich funkcji.
Fakt 4.5.5 (interpretacja fizyczna pochodnej funkcji wektorowej)
Niech oznacza wektor wodzący punktu materialnego w chwili t [t0,t1]. Wektor prędkości tego punktu wyraża się wzorem…
... zobacz całą notatkę






Komentarze użytkowników (0)