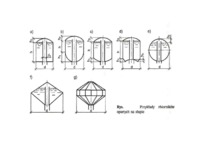
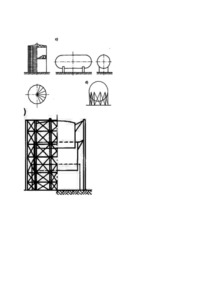
Zbiorniki tłokowe • Zbiorniki tłokowe, zwane suchymi, są lżejsze od dzwonowych i zapewniają bardziej wyrównane ciśnienie • Objętość tych zbiorników w warunkach krajowych wynosiła najczęściej 80 000 – 160 000 m3. • Zbiorniki tłokowe mają kształt graniastosłupa foremnego.Liczba boków podstawy j...
Zbiorniki wieżowe na wodę • Zbiorniki wieżowe mają za zadanie gromadzenie wody w systemie wodociągowym w celu zapewnienia odpowiedniej rezerwy w przypadku zwiększonego okresowego zużycia, a także zapewnienie odpowiedniego ciśnienia. • Metalowe zbiorniki wieżowe opierają się na stalowej konstru...
Zbiorniki wysokiego ciśnienia • Zbiornikami wysokiego ciśnienia lub zbiornikami ciśnieniowymi są zbiorniki na ciecze łatwo parujące lub gazy magazynowane przy nadciśnieniu większym od 0,05 MPa • Zbiorniki cylindryczne są podobne w kształcie do zbiorników poziomych na ciecze, różnią się tylko k...
ZBIORNIKI. Rodzaje zbiorników Ze względu na sposób użytkowania rozróżnia się zbiorniki do przechowywania cieczy lub gazów. Zbiorniki na ciecze służą najczęściej do przechowywania produktów naftowych, skroplonych gazów, cieczy pochodzenia organicznego, a także wody. Zbiorniki na ciecze mogą być bezc...
Dynamika konstrukcji Równania ruchu ukáadu dyskretnego (maáe drgania): M q(t ) C q(t ) K q(t ) F(t ) gdzie: q – wektor stopni swobody – uogólnionych przemieszczeĔ, funkcje czasu: q = q(t) M – macierz bezwáadnoĞci (mas) C – macierz táumienia K – macierz sztywnoĞci F – wektor obciąĪeĔ – ...
| 1 / [ / [ [ [ / [ [ [ K K / K K K K K [ K [ [ [ K [K /LQLRZH IXQNFMH NV]WDáWX PRĪHP\ RWU]\PDü NRU]\VWDMąF ] ZLHORPLDQyZ /DJUDQJH¶D 'OD GZyFK SXQNWyZ Z\NUHV ZLHORPLDQX EĊG]LH IXQNFMą OLQLRZą ...
1HXURQ ± SRGVWDZRZD MHGQRVWND XNáDGX QHUZRZHJR Z\ND]XMąFD ]GROQRĞFL Z\WZDU]DQLD L SU]HZRG]HQLD LPSXOVyZ QHUZRZ\FK ,GHD [ 7ELWyZ [ 3RáąF]HĔ 3RMHPQRĞü RN [ 7ELWyZ [ RSHUDFMLVHN [ PP POQ NP [ PP =LHPLD ± 6áRĔFH ...
\L \L LM § Q ) ¨ ¦ ZLM [ M EL ¨ ©M \ [ M LM ¦Z [ Q · § Q · ¸ ) ¨ ¦ ZLM [ M ¸ ¸ ¨ ¸ ¹ ©M ¹ EL EL M :[ ZL [ M ¦Z [ Q M ,PSOHPHQWDFMD GOD OLQLRZHM IXQNFML DNW\ZDFML QHXURQX :[ 5 L 7 L LM 7 M Q 7 M \ 'ZLM [ \ 7N M LM LM M 7 ...
0DFLHU] V]W\ZQRĞFL 361 i 0 3 T [ [ T K K [ ( 1 1 1 1 ) K ( 1 1 1 1 ) )XQNFMH NV]WDáWX Ni ( x y i) 1 4 1 [ i x 1 K i y NI ( x y i) Ni ( x y i) identity ( 2) ª 1 1 [ x 1 K y 0 « i i 4 NI ( x y i) simplify o « « ...
Pole naprężeń: σ(x) = {σx, σy, σz, τxy, τxz, τyz} Pole odkształceń: ε(x) = {εx, εy, εz, γxy, γxz, γyz} Pole przemieszczeń: u(x) = {ux, uy, uz} Punkt kontinuum: x = {x, y, z}, x ∈ Ω Mechanika kontinuum 2 µ - siły masowe (grawitacja, i...
