Mechanika gruntów - notatki z ćwiczeń
- Uniwersytet Przyrodniczy we Wrocławiu
- Mechanika gruntów
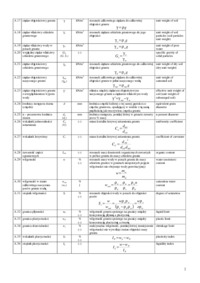
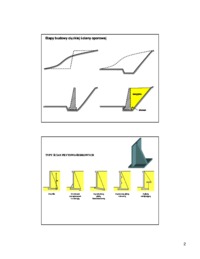
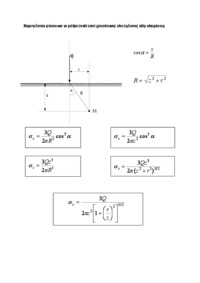
Ćwiczenie L4 Temat: Parametry wytrzymałościowe gruntów A. Na podstawie badań gruntów wykonanych w aparacie bezpośredniego ścinania wyznaczyć wartości kąta t...